# 149. Max Points on a Line
Given an array of points where points[i] = [xi, yi] represents a point on the X-Y plane, return the maximum number of points that lie on the same straight line.
Example 1:
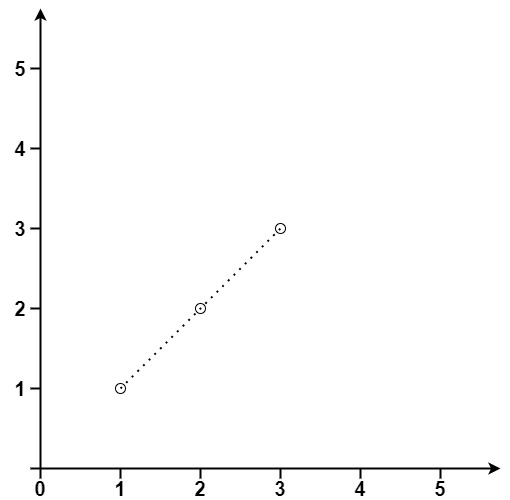
Input: points = [[1,1],[2,2],[3,3]]
Output: 3
Example 2:
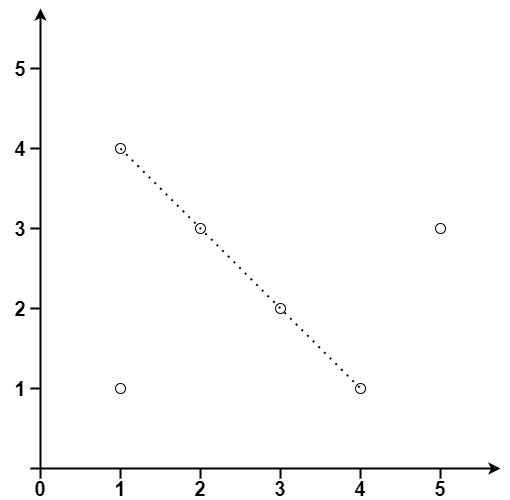
Input: points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
Output: 4
Constraints:
1 <= points.length <= 300points[i].length == 2-104 <= xi, yi <= 104- All the
pointsare unique.
# Answer
The obvious way is to make a map from lines to their points, this will requires time complexity since we are going through all lines by connecting every point with all other points. Space complexity would also be because we are storing all lines and corresponing points.
(Using double to represent slope k here is actually not optimal due to the nature of floating points, but it'll work for this question)
class Solution { public: int maxPoints(vector<vector<int>>& points) { if (points.size() <= 1) { return points.size(); } // y=kx+b // (k, (b, points set)) unordered_map<double, unordered_map<double, unordered_set<vector<int>*>>> lineCounts; // for x=... lines unordered_map<int, unordered_set<vector<int>*>> xLineCounts; for (int i = 0; i < points.size() - 1; i++) { for (int j = i + 1; j < points.size(); j++) { vector<int> &p1 = points[i], &p2 = points[j]; if (p1[0] == p2[0]) { if (xLineCounts.find(p1[0]) == xLineCounts.end()) { xLineCounts[p1[0]] = unordered_set<vector<int>*>(); } xLineCounts[p1[0]].insert(&p1); xLineCounts[p1[0]].insert(&p2); } else { double k = (double)(p1[1] - p2[1]) / (p1[0] - p2[0]); double b = (double)p1[1] - k * p1[0]; if (lineCounts.find(k) == lineCounts.end()) { lineCounts[k] = unordered_map<double,unordered_set<vector<int>*>>(); } if (lineCounts[k].find(b) == lineCounts[k].end()) { lineCounts[k][b] = unordered_set<vector<int>*>(); } lineCounts[k][b].insert(&p1); lineCounts[k][b].insert(&p2); } } } int maxVal = 0; for (auto &kb : lineCounts) { for (auto &bv : kb.second) { // cout << kb.first << ' ' << bv.first << ' ' << bv.second.size() << endl; maxVal = max(maxVal, (int)bv.second.size()); } } for (auto & xv: xLineCounts) { maxVal = max(maxVal, (int)xv.second.size()); } return maxVal; } };Runtime: 44 ms
Memory: 20.5 MB